Finding the number of roots using Rouché's Theorem

Translated with the help of ChatGPT and Google Translator

Yesterday, while watching YouTube, I found the following very interesting video. It was a video explaining how to find the number of roots within a certain region of a complex function using Rouché's Theorem.

#Definition

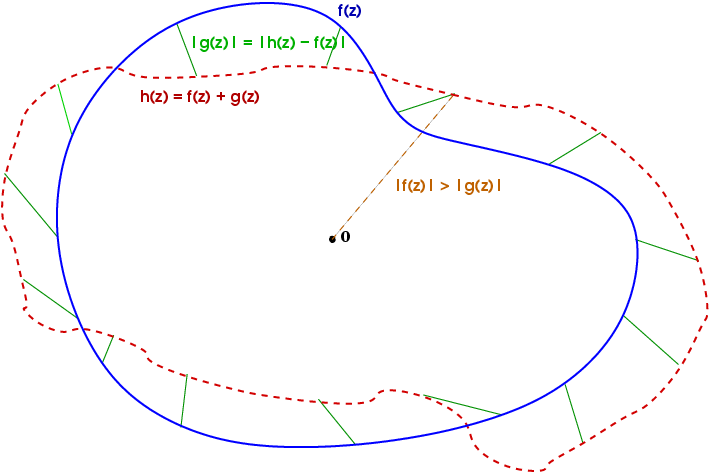
To briefly explain Rouché's Theorem explained in this video, it is as follows.

"If $|f(z)|>|g(z)|$ always holds true on the boundary $\partial D$ of a region $D$, then $f(z)$ and $f(z) inside D The number of roots of +g(z)$ is the same."

And when $|f|>|g|$ always holds, $f$ is said to be dominant over $g$.

Using this, when trying to find the number of roots of a complex polynomial function $h(z)$ within a certain region $D$, $h(z)$ is dominant, and the simple term $f$ and the non-dominant term $ We can easily solve the problem by dividing by g$.

#Example

Let's follow the example from the video above. We want to find the number of roots of the function $h(z)=z^5+3z^2+1$ where $D = \set{z|1<|z|<2}$.

To do so, set the area $D_1 = \{z | |z| <1\}, D_2 = \{z ||z|<2\}$, then subtract the number of roots in $D_1$ and $\partial D_1$ from the number of roots in $D_2$. .

First, regarding the number of roots inside each region, in $\partial D_1$, $|z|=1$, so $|z^5|=1, |3z^2|=3$, so $|z^5+1 |\leq|z^5|+1=2<|3z^2|$ holds true.

Therefore, $h$ can be divided by $f(z)=3z^2, g(z)=z^5+1$.

Therefore, the number of roots of $h(z)$ inside $D_1$ is 2, the same as the number of roots of $f(z)$. (middle root at $z=0$)

At this time, you should be careful that only the number of roots is the same, but the values of the roots are not the same. Therefore (in general) $h$ has no roots at $z=0$.

Similarly, $\partial D_2 = \{ z| |z|=2\}$ Above, $|z^5|=32>|3z^2|+1=4>|3z^2+1|$, so $f(z)=z^5, g( You can divide $h$ by z)=3z^2+1$.

Therefore, the number of roots of $h(z)$ inside $D_2$ is 5, the same as the number of roots of $f(z)$.

Finally, above $\partial D_1 = \{z||z|=1\}$, we just need to show that $h$ has no roots.

This also seemed to be a very simple method in the video above, as shown below.

If a root such as $|z|=1$ exists, then

$$z^5+3z^2+1=0\\ \therefore 3z^2=-z^5-1\\ \therefore |3z^2| = |z^5+1|\\ \therefore 3 = |z^5+1| < |z^5| + 1 = 2\\ \therefore 3<2$$

must be established. Obviously, this is false, so there is no such thing as $|z|=1$ such that $z^5+3z^2+1=0$.

In fact, this cannot but be established since $f(z)$ is dominant over $g(z)$ on $\partial D_1$. If a root exists on the boundary, $h=f+g = 0$, so $f=-g$ will hold, and therefore $|f|=|g|$, which means $f$ is not dominant.

Therefore, the number of roots inside $D_2$ - the number of roots on $\partial D_1$ - the number of roots inside $D_1$ = $5-0-2= 3$.