NACA Airfoil에 기반한 날개 모델링

추후 비행체를 한번 만들어 볼 계획입니다. 그때 제일 만들기 곤란한 부분이 날개일 듯해서 미리 날개 3D 모델을 생성하는 프로그램을 작성했습니다. 아래는 해당 레파지토리입니다.

https://github.com/unknownpgr/naca-airfoil-generator

Airfoil

날개에 있어서 가장 기본적인 사항은 그 날개 단면의 형상입니다. 날개 단면의 형상을 airfoil이라고 합니다. Airfoil은 물론 임의의 형상을 가질 수 있지만, 일반적으로는 다음과 같은 파라매터로 결정됩니다.

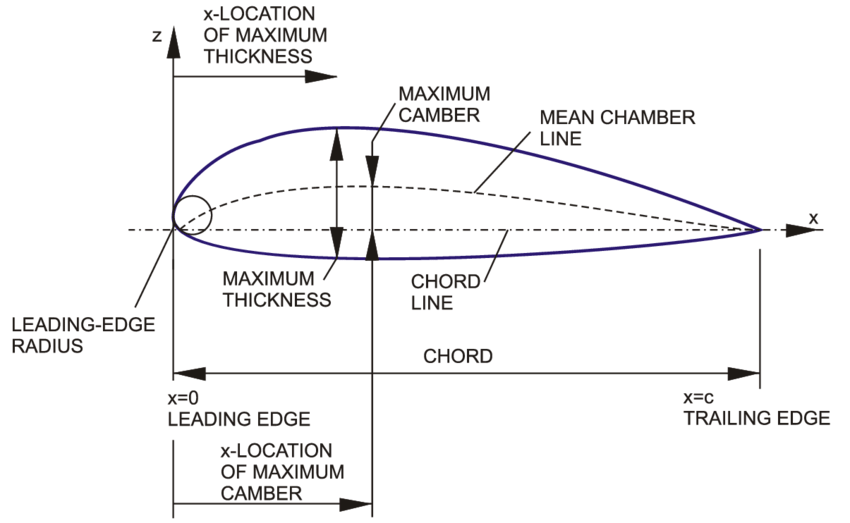
Airfoil

chord length: 날개 단면의 길이
thickness: 날개 단면의 두께
- maximum thickness: 날개 단면의 최대 두께
- maximum thickness position: 날개 단면의 최대 두께 위치
mean camber line: 날개 단면 중심선
- maximum camber: 날개 단면의 최대 곡률
- maximum camber position: 날개 단면의 최대 곡률 위치

이 airfoil의 형상을 나타내는 방법 중 하나가 NACA airfoil입니다. NACA란 National Advisory Committee for Aeronautics의 약자로, NACA airfoil은 미국의 항공기 연구기관이었던 NACA에서 개발한 airfoil 형상을 나타내는 방법입니다.

이 방법에 따르면 먼저 thickness는 아래와 같이 주어집니다.

$t(x) = 5t(0.2969\sqrt{x} - 0.1260x - 0.3516x^2 + 0.2843x^3 - 0.1015x^4)$

$x$ 는 chord에 대한 x축 거리의 비율로, 0과 1 사이의 값을 가집니다. 즉, $x=0$ 일 때 날개의 앞단, $x=1$ 일 때 날개의 뒷단을 나타냅니다.
$t$ 는 chord에 대한 날개 단면의 두께의 비율입니다.

camber line은 아래와 같이 주어집니다.

$y_c = \begin{cases} \frac{m}{p^2}(2px - x^2) & \text{if } 0 \leq x \leq p \\ \frac{m}{(1-p)^2}((1-2p) + 2px - x^2) & \text{if } p \leq x \leq 1 \end{cases}$

$m$ 은 maximum camber를 나타냅니다.
$p$ 는 maximum camber position을 나타냅니다.

그런데 이때 두께란 camber line으로부터 법선 방향으로의 두께를 말하는 것입니다. 이에 따라 upper surface와 lower surface는 아래와 같이 주어집니다.

$\begin{align*} x_u &= x - t(x)\sin(\theta) \\ y_u &= y_c + t(x)\cos(\theta) \\ x_l &= x + t(x)\sin(\theta) \\ y_l &= y_c - t(x)\cos(\theta) \end{align*}$

그러므로 NACA airfoil은 $m$ , $p$ , $t$ 세 개의 파라매터로 결정됩니다. 이 파라매터는 airfoil의 이름으로부터 알 수 있습니다. NACA airfoil은 네 개의 숫자로 이 값들을 표시하는데, 순서대로 $mptt$ 로 해석합니다. 예를 들어 NACA 2412는 $m=0.02$ , $p=0.4$ , $t=0.12$ 를 나타냅니다.

5자리 숫자인 경우도 있으며, 해석 방법이 다릅니다. 이에 대해서는 Wikipedia를 참고하세요.

Wing

날개의 단면을 결정했으면 이제 날개의 전체적인 형상을 결정해야 합니다. 날개의 형상은 다음과 같은 파라매터로 결정됩니다.

span(길이): 날개의 길이
aspect ratio(종횡비): 날개의 길이와 폭의 비율
taper ratio(테이퍼율): 날개의 앞단과 뒷단의 폭의 비율
angle of attack(받음각): chord와 수평선이 이루는 각도
dihedral angle(상반각): 항공기를 정면에서 봤을 때 날개가 위쪽(또는 아래쪽)으로 기울어진 각도
sweepback angle(후퇴각): 날개가 뒤쪽으로 젖혀진 각도

이 외에도 twist나 winglet 등 다양한 형상 파라매터가 있을 수 있지만 계산을 너무 복잡하게 만들기 때문에 지금은 고려하지 않기로 했습니다.

이 파라매터들을 이용하여 날개의 형상을 결정할 수 있습니다. 이것은 단순히 airfoil을 구한 것을 span 방향으로 확장하면서 회전이나 폭의 변화를 주는 것으로 쉽게 구현할 수 있습니다.

Model Generation

이제 이로부터 날개의 3D 모델을 생성하기 위해서는 이 수식으로부터 메시(mesh)를 생성해야 합니다. 메시는 주어진 표면을 삼각형으로 분할하는 그래프로, 점(vertex)와 점 3개로 이루어진 면(face)로 구성됩니다. 메시를 조밀하게 구성하면 모델이 더욱 정확해지며 부드러워지는 반면 연산량이 기하급수적으로 늘어납니다. 반면 메시를 성기게 구성하면 연산량이 줄어들지만 모델이 부정확해질 수 있습니다. 이에 따라 다음과 같은 간단한 알고리즘을 고안했습니다.

Initial Algorithm

날개의 표면을 parametric function $F(u, v)$ 로 표현합니다. ( $u\in[0,1]$ , $v\in[0,1]$ )
face = [ (0,0), (0,1), (1,0), (1,1) ] 로 초기화하고 다음 과정을 반복합니다.
1. face의 각 점을 $F(u, v)$ 로 변환합니다.
2. face가 충분히 평평한지 확인합니다.
3. face가 충분히 평평하다면 face를 메시에 추가합니다.
4. face가 충분히 평평하지 않다면 face를 4등분으로 분할합니다. 분할 시에는 각 edge의 중점과 사각형의 중간 지점으로 이루어진 5개의 노드가 추가됩니다.
5. 각 분할에 대해 다시 1번 과정을 반복합니다.

Problem

그런데 이 방식을 사용하면 다음과 같은 문제가 발생합니다.

중복되는 노드가 많이 발생합니다.
에지의 포함 관계 정보를 잃어버리게 됩니다.

예를 들어서 도메인상에 아래와 같은 face의 분할이 주어졌다고 가정하겠습니다.

┌───┬───┬───────┐
│   │   │       │
├───┼───┤   d   │
│   │ a │       │
├───┼───┼───────┤
│   │ b │       │
├───┼───┤       │
│   │ c │       │
└───┴───┴───────┘

이때 a의 왼쪽 아래 노드와 b의 읜쪽 위 노드는 실제로는 같은 노드입니다. 그러나 위 알고리즘을 그대로 사용하면 이 두 노드를 다른 노드로 취급하게 됩니다.
c의 아래쪽 노드는 원래는 초기 사각형의 아래쪽 에지에 포함된 노드이지만 그 정보를 잃어버리게 됩니다. 초기 에지의 정보는 모델이 surface가 아니라 닫힌 도형인 경우이거나 두 개 이상의 모델을 결합할 때 반드시 필요합니다.
a의 오른쪽 위 노드는 d의 왼쪽 edge에 포함되어 있습니다. 그러나 이런 정보도 잃어버리게 됩니다. 그러므로 a의 오른쪽 에지와 d의 왼쪽 에지가 서로 연결되지 않습니다.

Improved Algorithm

이러한 문제를 해결하기 위해 에지를 tree로 저장하는 방식을 고안했습니다. 이 방식은 다음과 같습니다.

edge는 반드시 좌측에서 우측으로, 또는 아래에서 위로 향합니다. ( $x_2\geq x_1 \land y_2\geq y_1$ )
edge는 시작 노드, 끝 노드를 가집니다. 만약 edge가 더 나누어질 수 있는 경우 edge는 left child, right child를 가집니다. left child는 edge의 시작 노드와 edge의 중간 지점을 잇는 edge입니다. right child는 edge의 중간 지점과 edge의 끝 노드를 잇는 edge입니다.

이것을 json 형식으로 표현해보면 아래와 같습니다.

// Edge without children
{
  "start": 1, // index of start node
  "end": 2, // index of end node
  "children": []
}

// Edge with children
{
  "start": 1,
  "end": 2,
  "children": [
    // Left child
    {
      "start": 1,
      "end": 3,
      "children": []
    },
    // Right child
    {
      "start": 3,
      "end": 2,
      "children": []
    }
  ]
}

이제 edge를 반으로 나눠야 할 때 다음과 같은 알고리즘을 사용합니다.

edge가 이미 나눠진 경우 left child와 right child를 그대로 반환합니다.
edge가 나눠지지 않은 경우
1. 중간 지점의 노드를 새로 생성합니다.
2. left child (start, middle)와 right child (middle, end)를 생성합니다.
left child와 right child를 반환합니다.

이것을 python pseudocode로 나타내면 아래와 같습니다.

def divide_edge(edge):
    index_start, index_end, children = edge

    if len(children) == 2:
        return children

    start = points[index_start]
    end = points[index_end]
    middle = (start + end) / 2
    points.append(middle)
    index_middle = len(points) - 1

    child_start = [index_start, index_middle, []]
    child_end = [index_middle, index_end, []]
    children.append(child_start)
    children.append(child_end)

    return children

이 방식을 사용하면 중복되는 노드가 발생하지 않으며, 에지의 포함 관계 정보도 잃어버리지 않습니다.

Flatness Check

다음으로 face가 충분히 평평한지 확인하는 방법을 고안해야 합니다. 이때 face가 충분히 평평하다는 것은 두 가지 조건을 만족해야 합니다.

face들의 모든 점이 거의 같은 평면에 있어야 합니다.
face가 convex해야 합니다.

만약 첫 번째 조건만 체크한다면 정의역에서의 사각형이 공역에서 U 모양으로 변하는 경우에도 도형이 평평하다고 판단하여 더 분할이 이루어지지 않게 되고, 따라서 따라서 convex하지 않은 평면이 convex하게 변환되는 문제가 발생할 수 있습니다. 이로부터 다음과 같은 알고리즘을 고안했습니다. 먼저 다음과 같이 face와 vertices가 주어집니다.

a────b
│    │
│    │
c────d

face 내부에는 적당한 sample point들이 주어집니다. 저는 아래와 같이 9개의 sample point를 사용했습니다.

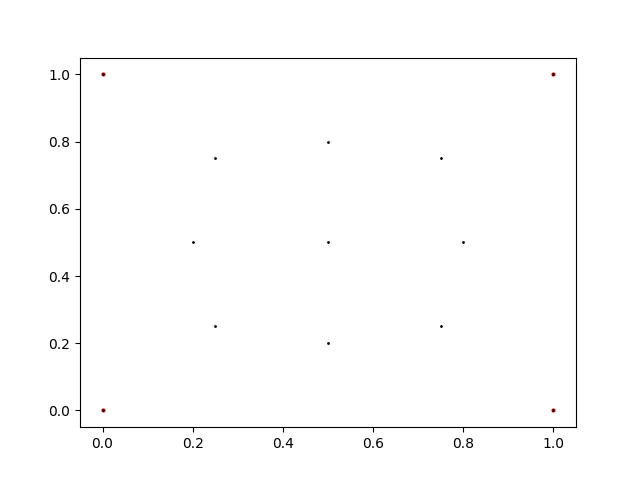
먼저 계산을 쉽게 하기 위해 face를 $z=0$ 평면으로 변환합니다.

sample point를 포함한 face의 모든 점을 $F(u, v)$ 로 변환합니다. 변환한 점들을 각각 $a$ , $b$ , $c$ , $d$ 라고 부르겠습니다.
$ad$ $a d$ 와 $bc$ $b c$ 의 cross product를 계산한 후, 이것의 길이가 1이 되도록 정규화합니다. 이것을 평면의 face의 법선벡터라고 가정합니다.
- 만약 실제로 $a, b, c, d$ 가 평면을 이룬다면 이것은 정확한 계산이지만, 일반적으로는 그렇지 않습니다.
평면의 법선벡터와 벡터 $ad$ 로부터 Gram-Schmidt process를 통해 평면의 기저를 구합니다.
평면의 법선벡터가 $z$ 축이 되고 $a$ 가 원점이 되도록 평면을 변환합니다.

다음으로 이 face가 convex한지를 검사합니다. 그런데 닫힌 곡선의 convexity는 오직 2차원에서만 정의됩니다. 그런데 앞의 과정에서 변환한 점들은 한 평면 위에 있지 않습니다. 그래서 위 방법을 적용하기 전에 먼저 각 점들을 평면에 사영한 후 convexity를 검사합니다. face가 convex하려면 다음 조건을 모두 만족해야 합니다.

도형 안의 test point들이 벡터 $ad$ 와 벡터 $ab$ 의 선형 결합으로 표현됩니다.
그 계수가 모두 0 이상이어야 합니다.
그 계수가 모두 1 이하여야 합니다.

다음으로 face가 충분히 평평한지를 검사합니다. face가 평평하다는 것은 sample point들의 z값이 거의 0이라는 것이므로, sample point들의 z값이 충분히 작다면 face가 평평하다고 판단합니다.

위 알고리즘에서 convex check부분은 face와 sample point들이 평면이라고 가정한 후 계산을 진행하므로 만약 face가 곡률이 큰 곡면이라면 잘못된 답을 얻을 수도 있습니다. 그러나 convex check를 통과하더라도 마지막에 flatness를 검사하기 때문에 이러한 문제를 피할 수 있습니다. convex check를 flatness check보다 먼저 하는 이유는 convex check가 flatness check보다 더 강한 조건이기 때문입니다. 만약 face가 충분히 flat하다고 해도 convex하지 않으면 그 face는 flat하다고 판단해서는 안 됩니다. 반면 convex하지 않은 face는 flat하더라도 곧바로 flat하지 않다고 판단할 수 있습니다. 아래는 이것을 구현한 실제 코드입니다.

def __test_flatness(self, rect, func):
    """
    Test the flatness (linearity) of the given rect.
    """
    test_inputs = self.__test_weights @ rect
    test_outputs = func(test_inputs)

    """
    The transformed shape should be planar.
    It means that there exists a plane that contains all the points.

    A plane is determined by center point and normal vector.
    We can roughly assume that the center point is the average of the
    first four points, and the normal vector is the cross product of diagonals.
    """

    ps = test_outputs[:4]
    normal = np.cross(ps[0] - ps[3], ps[1] - ps[2])
    normal /= np.linalg.norm(normal)

    """
    Before calculating, for the ease of calculation, we can
    move the plane to be the z=0 plane.
    """

    test_outputs -= test_outputs[0]
    original_z = normal
    original_x = ps[0] - ps[3]
    original_x /= np.linalg.norm(original_x)
    original_y = np.cross(original_z, original_x)
    original_basis = np.vstack([original_x, original_y, original_z])
    original_basis_inv = np.linalg.inv(original_basis)
    test_outputs = test_outputs @ original_basis_inv

    """
    Before calculating the distance, we must check that the transformed shape is convex.
    It means that the other points can be represented as the convex combination of the first four points.
    we should flatten the points to the plane because the points are not on same plane in general.
    """

    flattened_points = test_outputs[:, :2]
    basis = flattened_points[1:3]
    test_points = flattened_points[4:]
    a = np.linalg.lstsq(basis.T, test_points.T, rcond=None)[0].T
    if np.any(a < 0) or np.any(a > 1):
        return np.inf

    """
    Because the plane is now the z=0 plane, the distance of the points to the plane
    is simply the z-coordinate of the points.
    """

    distances = test_outputs[:, 2]

    """
    The flatness of the shape is the maximum distance of the points to the plane.
    """

    return np.max(np.abs(distances))

Weaving

닫힌 도형을 만들고자 하는 경우 두 에지를 하나의 에지로 합쳐야 합니다. 이때 두 에지가 서로 일치하도록 만들면 겉으로 보기에는 닫힌 도형이 되지만, 3D 모델링 툴이나 3D 프린터 슬라이서는 이것을 닫힌 도형으로 인식하지 않을 수 있습니다. 그러므로 두 에지 사이에 face를 추가해야 합니다. 이때 두 에지는 서로 다른 개수의 node로 이루어질 수 있기 때문에 간단히 삼각형으로 나눌 수는 없습니다. 이에 따라 다음과 같은 알고리즘을 사용했습니다. 이것은 two-pointer 방식으로 최대한 꼬임이 없도록 두 edge 사이에 face를 추가하는 알고리즘입니다.

def weave_edges(self, edge1, edge2, reverse_face=False):
    vs1 = self.vertices[edge1]
    vs2 = self.vertices[edge2]

    new_faces = []
    i1 = 0
    i2 = 0

    norm = lambda v: np.linalg.norm(v)

    while i1 < len(vs1) - 1 or i2 < len(vs2) - 1:
        if i1 == len(vs1) - 1:
            new_faces.append([edge1[i1], edge2[i2], edge2[i2 + 1]])
            i2 += 1
            continue
        if i2 == len(vs2) - 1:
            new_faces.append([edge1[i1], edge2[i2], edge1[i1 + 1]])
            i1 += 1
            continue
        if norm(vs1[i1] - vs2[i2]) < norm(vs1[i1 + 1] - vs2[i2]):
            new_faces.append([edge1[i1], edge2[i2], edge2[i2 + 1]])
            i2 += 1
        else:
            new_faces.append([edge1[i1], edge2[i2], edge1[i1 + 1]])
            i1 += 1

    if reverse_face:
        new_faces = [f[::-1] for f in new_faces]

    self.faces = np.vstack([self.faces, new_faces])

Triangulation

마지막으로, 이런 방식으로 구성한 face는 반드시 4개 이상의 노드로 구성됩니다. 만약 face가 4개의 노드로 구성된다면 간단히 대각선으로 나누고, 5개 이상의 노드로 구성된다면 face의 한 가운데에 edge 노드들의 평균인 새로운 노드를 추가하고 이 노드를 기준으로 face를 나누는 방식으로 triangulation을 수행합니다.

ear-clipping 등 새로운 노드를 추가하지 않는 방식이 있지만, 다음과 같은 이유로 위 방식을 사용했습니다.

이 글에서 설명한 방법대로 face를 구성하게 되면 여러 노드가 한 직선 위에 오는 경우가 많습니다.
그런 경우 새로운 노드를 추가하지 않으면 face 사이에 날카로운 벽이 생기게 됩니다.
앞서 face에서 convex 검사를 수행했기 때문에 중점이 face 내부에 포함되는 것이 보장됩니다.

Result

아래는 위 알고리즘을 사용하여 생성한 3D 모델입니다.

모델 곳곳에 빈 공간이 보이는데, 이것은 matplotlib의 렌더링 오류입니다. 실제로는 이런 문제가 없습니다.

아래는 위 모델을 구성하기 위한 mesh입니다.

모델의 왼쪽 면과 오른쪽 면을 닫았기 때문에 선이 겹쳐져 진하게 표시됩니다.
모델의 위쪽 면과 아래쪽 면을 연결했기 때문에 모델을 위아래로 가로지르는 선들이 보입니다.

NACA Airfoil에 기반한 날개 모델링

Airfoil

Wing

Model Generation

Initial Algorithm

Problem

Improved Algorithm

Flatness Check

Weaving

Triangulation

Result

References