베이즈 정리에 기반한 라인 센서 알고리즘 구현

라인 센서란 라인트레이서형 로봇에서 사용되는 센서로, 로봇이 라인을 따라갈 수 있도록 센서의 중심으로부터 상대적인 라인의 위치를 추정하는 데 사용된다.

라인 센서는 여러 형태로 구현될 수 있다. 여기서는 그중 아래 예시와 같이 여러 개의 Infrared (IR) 센서를 일렬로 나열하여 사용할 때 라인의 위치를 추정하는 알고리즘을 다룬다.

IR0---IR1---IR2---IR3---IR4---IR5---IR6---IR7

논의에 앞서 각 IR센서의 위치 $x_n$에 대하여 IR0의 위치는 -1, IR7의 위치는 1로 정의하자. 즉 $x_n=2n/7-1$이라 하자.

기존 알고리즘

내가 활동하는 로봇 동아리 제틴에서는 아래와 같이 weighted average를 사용하여 라인의 위치를 추정하였다.

센서 값 $v_n$에 대하여 아무것도 없는 검은 바탕을 감지할 때 센서 값이 0, 흰 라인 위에 센서가 정확히 올라갈 때 값이 1이라 하자. 라인의 경계에 위치한 센서의 값은 0과 1 사이의 값이 된다.

이때 기존에는 위치에 센서 값으로 weight를 주어서 다음과 같이 라인의 위치를 추정하였다.

$$\hat{x} = \frac{\sum_{n=0}^7 x_nv_n}{\sum_{n=0}^7 v_n}$$

이 방법은 대단히 간단하지만 잡음이 포함되는 경우 라인 위치를 크게 잘못 추정할 수 있다. 이를 개선하기 위해 베이즈 정리를 이용하여 라인 위치를 추정하는 알고리즘을 구현하였다.

베이즈 정리

베이즈 정리는 다음과 같다.

$$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$$

이 식에서

• $P(A)$를 사전 확률(prior probability),
• $P(A|B)$를 사후 확률(posterior probability),
• $P(B|A)$를 가능도(likelihood),
• $P(B)$를 증거(evidence)라고 한다.

이때 만약 $P(B)$가 $P(A)$에 의존하는 사건이면 전체 확률의 법칙을 이용하여 다음과 같이 정리된다.

$$P(A|B) = \frac{P(B|A)P(A)}{\sum_{A}P(B|A)P(A)}$$

분포가 연속확률분포이면 다음과 같이 표현된다.

$$P(A|B) = \frac{P(B|A)P(A)}{\int_{A}P(B|A)P(A)dA}$$

베이즈 정리를 이용한 라인 추정

알고자 하는 것은 센서 8개의 값 $\vec v= (v_0, v_1, \cdots, v_7)$이 주어졌을 때 라인의 위치 $p$이다. 이를 위해서 라인의 위치 $p$에 대한 확률밀도함수를 구하고 그중 가장 높은 값을 가지는 $p$값을 선택할 것이다. 이러한 확률밀도는 센서 값들이 주어졌을 때 센서 위치의 분포를 추정하는 것이므로 조건부 확률 $P(p|\vec v)$로 표현된다. 그런데 이 조건부 확률을 알지 못하므로 아래와 같이 앞서 정리한 연속확률분포의 베이즈 정리를 이용하여 이 확률분포를 구할 것이다.

$$P(p|\vec v) = \frac{P(\vec v|p)P(p)}{\int_{p}P(\vec v|p)P(p)dp}$$

이 식에서 사전 확률 $P(p)$를 정하기 위해서는 센서 값의 분포를 측정해야 한다. 라인 추종형 로봇은 라인 위치가 0이 되도록 추종하므로 실제 센서의 값은 0을 중심으로 하는 분포를 가질 것이다. 그러나 여기서는 범용성을 위해 이러한 가정 대신 적당한 범위에서 균등 분포를 가진다고 가정하자. 이때 이 범위는 $[-1,1]$보다 조금 더 커도 되는데, 왜냐하면 가장 바깥 쪽 센서보다 라인이 살짝 밖에 있는 경우에도 센서가 라인을 감지할 수 있기 때문이다. (이것 역시 기존 알고리즘과의 차이로, 기존 알고리즘에서 라인의 위치는 반드시 $[-1,1]$ 내에 있다.)

즉, 그러한 범위 내에서 $P(p)=k$이다. 이에 따라 식은 다음과 같이 변형된다.

$$P(p|\vec v) = \frac{P(\vec v|p)}{\int_{p}P(\vec v|p)dp}$$

이로부터 $P(\vec v|p)$만 구하면 곧바로 확률분포를 추정할 수 있다. 그리고 위 식의 분모가 상수이기 때문에 위 식을 최대화하는 $p$를 구하는 것은 $P(\vec v|p)$를 최대화하는 $p$를 구하는 것과 같다.

상기한 것처럼 베이즈 정리에서 $P(\vec v|p)$를 우도(likelihood)라고 한다. 그러므로 이러한 방식을 **최대우도법(Maximum Likelihood Estimation, MLE)**이라고 한다.

다만 최대우도법은 보통 확률변수를 같은 확률분포에서 표집한 것을 가정한다. 하지만 이 경우에는 센서 위치에 따라 값의 확률분포가 서로 다르므로 일반적인 최대우도법과는 차이가 있다. 그러나 근본적으로 우도를 최대화함으로서 모수-이 경우 라인 위치-를 추정하는 것은 같으므로 이 접근법을 최대우도법이라 불러도 무방할 것이다.)

이를 구하기 위해 센서 하나에 대하여 라인과 센서의 거리에 따른 센서 값의 확률분포를 구한 뒤, 이를 센서 값 벡터에 대한 확률분포로 확장할 것이다.

먼저 거리가 $d$ 떨어진 센서에 대하여 센서 값이 $v$일 확률 분포, 즉 확률밀도함수를 $f_d(v)$라고 나타내자. 이때 이것이 단일한 값이 아니라 확률분포로 나타나는 이유는 잡음에 의한 것이다. 이러한 잡음을 서로 독립이라고 가정하자. (실제로는 모든 센서에 비슷한 영향을 미치는 잡음원(외부광 등)이 있으므로 독립이 아닐 것이나, 독립이라 가정해도 무방할 것이다.) 그러면 센서 값 벡터에 대한 확률분포$P(\vec v|p)$는 다음과 같이 표현된다.

$$P(\vec v|p) = \prod_{n} f_{|x_n-p|}(v_n)\\$$

즉,

1. 라인의 위치가 주어질 때
2. 이로부터 예상되는 각 센서 값의 확률밀도함수에
3. 실제 센서 값을 넣어 얻은 확률밀도의
4. 곱으로 표현된다.

이것이 올바른 확률분포인지는 그 적분이 1이 되는지를 확인해보면 된다. 이는 푸비니의 정리에 따라 다음과 같이 1이 됨을 보일 수 있다.

$$\begin{align} \int_v P(\vec v|p)dv &=\int_{v_1}\int_{v_2}\cdots\int_{v_n}\prod_{n} f_{|x_n-p|}(v_n)dv_1dv_2\cdots dv_n \\ &= \prod_{n} \int_{v_n} f_{|x_n-p|}(v_n)dv_n\\ &= \prod_{n} 1\\ &=1 \end{align}$$

푸비니의 정리란 리만 적분에서 정사각형 영역 $R$에 대하여 $f(x,y)$가 연속이면 아래 등식이 성립한다는 정리이다.

$$\int_R f(x,y)dA = \int_a^b\int_c^d f(x,y)dxdy$$

이로부터 $f(x,y)$가 두 함수의 곱 $f_1(x)f_2(y)$으로 표현되는 경우 아래 등식이 성립힌다.

$$\int_R f(x,y)dA = \int_a^b\int_c^d f_1(x)f_2(y)dxdy = \int_a^b f_1(x)dx\int_c^d f_2(y)dy$$

이는 쉽게 고차원으로 확장할 수 있다.

그러므로 얻은 $P(\vec v|p)$를 위의 식에 대입하면 다음과 같이 정리된다.

$$P(p|\vec v) = \frac{\prod_{n} f(v_n, |x_n-p|)}{\int_{p}\prod_{n} f(v_n, |x_n-p|)dp}$$

이로부터 알고자 하는 것은 이 값을 최대화하는 $p$이다. 이때 이 식의 분모는 상수이므로 이를 최대화하는 것은 분자를 최대화하는 것과 같다. 그러므로 다음과 같이 정리된다.

$$\hat{p} = \arg\max_p \prod_{n} f(v_n, |x_n-p|)$$

위 식은 확률밀도함수를 여러 번 곱하여 얻어지므로 숫자가 대단히 크거나 작아질 수 있다. 그러므로 로그 변환하여 다음과 같이 정리한다.

$$\hat{p} = \arg\max_p \sum_{n} \log f(v_n, |x_n-p|)$$

실험

이를 Python으로 구현하여 실험해보았다. 실험을 위하여 거리에 따른 센서 값의 확률밀도함수를 다음과 같이 정의하였다.

$$v\sim\mathcal{N}(\mu, 0.1)\\ \mu=\max(1-3|d|,0)$$

실제 라인 위치를 0.64로 두면 아래와 같이 센서 값이 측정된다.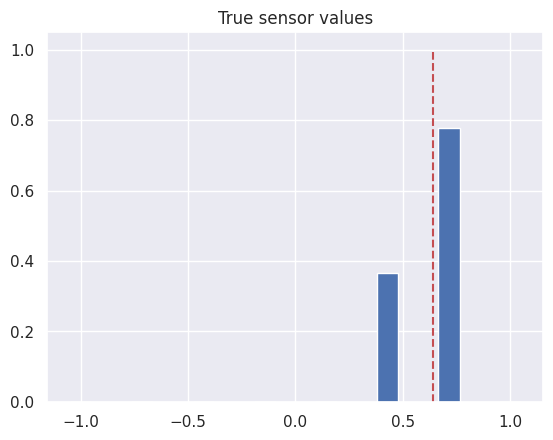

그런데 실제 센서에는 잡음이 필연적으로 포함되므로 정규분포 잡음을 추가하였다.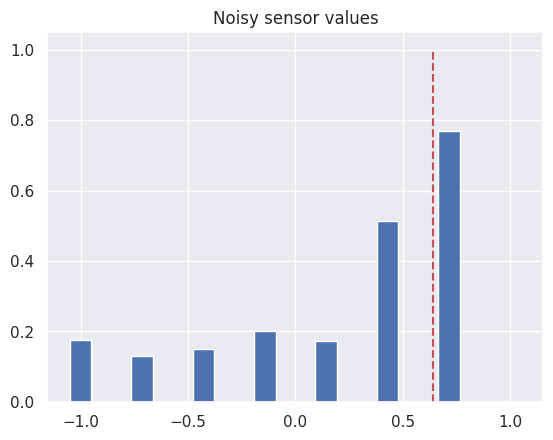

이로부터 라인 위치를 추정하면 다음과 같다.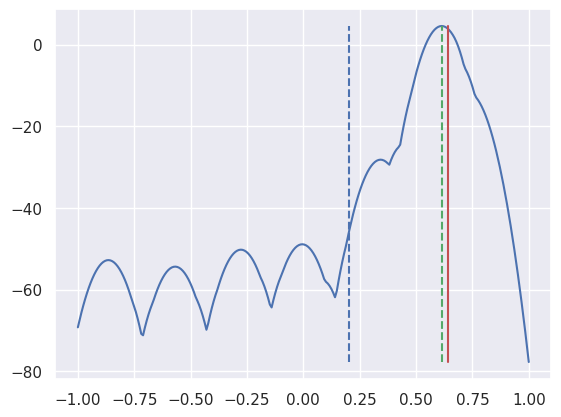

• 붉은 실선은 실제 라인 위치를 나타낸다.
• 파란 곡선은 예상되는 라인 위치의 로그 우도(likelihood)를 나타낸다.
• 초록색 점선은 이로부터 추정된 라인 위치를 나타낸다.
• 파란색 점선은 예전 알고리즘으로부터 추정된 라인 위치를 나타낸다.

이를 통해 새로운 알고리즘이 기존 알고리즘보다 더 정확하게 라인 위치를 추정한다는 것을 알 수 있다.

최적화

이는 여러 번의 지수, 로그 연산 등을 이용하므로 임베디드 시스템에서 계산하기에는 계산량이 너무 클 수 있다. 그리고 값이 대단히 작을 수 있어 부동소수점 연산에 따른 오차가 발생할 수 있다.

이때 다음과 같은 몇 가지 가정을 통하여 이를 최적화할 수 있다.

1. 센서 값의 확률밀도함수가 정규분포라고 가정한다.
2. 분포의 평균은 라인 위치에 대한 함수이다.
3. 분포의 표준편차는 상수다.
4. 센서 값은 센서 간 독립이다.

이러한 가정으로부터 센서와 라인의 거리 $x$에 대한 센서 값 분포의 평균을 $\mu(x)$, 표준편차를 $\sigma$라 하자. 그러면 센서 값의 확률밀도함수는 다음과 같이 정리된다.

$$f(v,x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(v-\mu(x))^2}{2\sigma^2}\right)$$

다음으로 각 센서의 위치를 $p_n$, 측정된 센서 값을 $v_n$이라 하자. 그러면 $p(v|x)$는 다음과 같이 정리된다.

$$\begin{align} p(v|x) &= \prod_{n} f(v_n, |x-p_n|)\\ &= \prod_{n} \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(v_n-\mu(|x-p_n|))^2}{2\sigma^2}\right) \end{align}$$

그러므로 이 식에 로그를 씌운 로그 우도는 다음과 같이 정리된다.

$$\begin{align} \log p(v|x) &= \sum_{n} \log \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(v_n-\mu(|x-p_n|))^2}{2\sigma^2}\right)\\ &= \sum_{n} \left(\log \frac{1}{\sqrt{2\pi}\sigma}-\frac{(v_n-\mu(|x-p_n|))^2}{2\sigma^2}\right)\\ &= -\sum_{n} \left(\log \sqrt{2\pi}\sigma+\frac{(v_n-\mu(|x-p_n|))^2}{2\sigma^2}\right)\\ &= -n\log \sqrt{2\pi}\sigma-\frac{1}{2\sigma^2}\sum_{n} (v_n-\mu(|x-p_n|))^2 \end{align}$$

그런데 구하고자 하는 것은 이 식을 최대화하는 $x$이다. 따라서 상수항과 상수 곱을 무시하면 다음과 같이 정리된다. (부호를 바꾸면서 argmax가 argmin으로 바뀐 것에 유의하라.)

$$\begin{align} \hat{x} &= \arg\min_x \sum_{n} (v_n-\mu(|x-p_n|))^2\\ \end{align}$$

이로부터 이 식이 센서의 표준편차와 무관하다는 것을 확인할 수 있다.

정리해보면 다음과 같이 실제 로봇에 적용할 수 있다. 먼저 튜닝 단계에서 다음을 수행한다.

1. 센서와 라인의 거리 $d$를 바꿔가며 센서 값 $v$를 측정한다. 이때 한 위치에서 외부광을 주거나 라인의 각도를 약간씩 바꾸는 등 여러 잡음을 주어 가며 측정한다.
2. $d$에 따른 $v$의 평균을 나타내는 함수 $\mu(d)$를 구한다. 가장 좋은 것은 센서와 라인의 거리에 따른 물리 모델을 구한 후 실측값에 따라 파라매터를 튜닝하는 것이다. 그러나 그냥 실측값을 linear interpolation하거나 적당한 곡선에 대해 curve fitting하는 것도 괜찮을 것이다.

이로부터 추론 단계에서는 다음을 수행한다.

1. 측정된 센서 값 $v_n$을 구한다.
2. 가능한 $x$값들을 순회하면서 $\sum_{n} (v_n-\mu(|x-p_n|))^2$을 최대화하는 $x$를 계산한다. ($p_n$은 센서의 위치이다.)

• 이는 대단히 간단하여 C언어 등으로도 충분히 구현할 수 있다.
• 또한 이 최적화를 통하여 기존에 약 1.14초가 소요되던 계산을 0.0004초까지 줄일 수 있었다.
• 계산에 로그나 지수 등이 사용되지 않으므로 부동소수점보다 덜 정밀한 연산을 사용할 수 있다. 적절히 범위를 조절하면 정수 연산으로도 충분히 구현할 수 있을 것이다.

아래는 이를 Python으로 구현한 것이다.

import numpy as np

def mu(ds):
    ds = 1-np.abs(ds)*3
    ds = np.maximum(ds,0)
    return ds

def optimized(values,positions,mu,xs):
    n = len(values)
    result = np.zeros(len(xs))
    for i in range(n):
        result += (values[i]-mu(xs-positions[i]))**2
    return result

vs = [ ... ] # measured sensor values
ps = np.linspace(-1,1,8) # sensor positions
xs = np.linspace(-1,1,300) # candidate positions
ys = optimized(vs,ps,mu,xs) # log likelihood
x_hat = xs[np.argmin(ys)] # estimated position

아래는 위 코드의 결과를 시각화한 것이다. 마찬가지로 붉은 실선은 실제 라인 위치를 나타내고, 초록색 점선은 이로부터 추정된 라인 위치를 나타낸다. (사용된 센서 값은 위와 다르다.)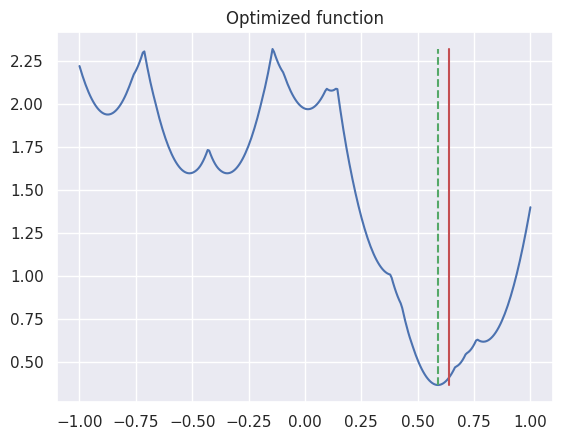

결론

• 베이즈 정리를 이용하여 라인 센서의 위치를 추정하는 알고리즘을 구현하였다.
• 이를 통해 기존 알고리즘보다 더 정확하게 라인 위치를 추정할 수 있었다.
• 또한 이를 최적화하여 계산량을 줄일 수 있었다.