다음 문제로 뭘 풀까 하다가 양심없게도 알고리즘 소모임에서 이번에 진행하는 LeetCode 문제를 보고 풀어보기로 했습니다. 오늘 풀어 본 문제는 반복되는 문자가 없는 가장 긴 부분문자열이라는 문제인데요. 말 그대로

주어진 문자열의 연속되는 부분 문자열 중
반복되는 문자가 하나도 없는 것들 중
가장 긴 것의 길이는?

이라는 문제였습니다.

$O(n^2)$ 접근

저는 처음에 이것이 $O(n^2)$ 시간/공간복잡도를 필요로 하는 dynamic programming 문제인줄로만 생각했습니다. 그래서 dp라는 이름의 2차원 배열을 만들고, dp[s][e]를 채웠습니다. dp[s][e]는

만약 주어진 문자열에서 s 번째에서 시작해서 e번째에서 끝나는 부분 문자열이 반복되는 문자가 없을 경우
- 그 부분 문자열을 값을 가지고
반복되는 문자가 있을 경우
- False를 값으로 가집니다.

이렇게 구성할 경우, dp[s][e]의 값을 알아내려면 dp[s+1][e]와 dp[s][e-1]의 값만 알면 됩니다. 그러므로 dp[x][x]=str[x]로 초기화하고 점차 이 배열을 채워나가면서 문자열 길이 = e-s+1의 최댓값을 구하면 됩니다.

(실제로는 dp[s][e]에는 문자열 전체가 아니라 시작 문자와 끝 문자만 저장되면 됩니다. 그러나 이 알고리즘은 실패한 알고리즘이므로 아이디어만 설명하고 넘어갑니다.)

이 알고리즘은 dp배열을 구상하고 채우는 것이 약간 복잡할 뿐, 아이디어만 떠올리면 별로 어렵지 않습니다. 그래서 금방 python으로 코딩한 후, 제출해봤습니다. 아래는 소스코드입니다.

class Solution(object):
    def lengthOfLongestSubstring(self, st):
        """
        :type s: str
        :rtype: int
        """
        l = len(st)
        if l==0:
            return 0
        dp = [[False]*l for _ in range(l)]
        '''
        dp[s][e] = substr[s][e] including s,e
        '''
        for i in range(l):
            dp[i][i] = st[i]
        ml = 1
        for i in range(1,l):
#           i = string length - 1
            trueFlag = False
            for j in range(l-i):
                s = j
                e = s+i
                a = dp[s+1][e]
                b = dp[s][e-1]
                if (a is not False) and (b is not False) and (b[0] is not a[-1]):
                    ml = i+1
                    dp[s][e] = st[s]+st[e]
                    trueFlag = True
                else:
                    dp[s][e] = False
            if not trueFlag:
                return ml
        return ml

결과는...

하나가 시간이 부족해서 안 되네요. 맞왜틀을 몇 번 시전하고 난 후, 입력을 자세히 살펴보니 아래와 같은 문자열이 계속 반복되고 있었습니다. (LeetCode에서는 친절하게도 실패한 입력이 무엇인지를 알려줬습니다.)

abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789!\"#$%&'()*+,-./:;<=>?@[\\]^_`{|}~

그러므로 전체 문자열 길이가 $m$ 이라 하고, 이 문자열의 길이가 $k$ 라 하면 길이 $k$ 미만의 부분 문자열에서는 반복이 절대 나타나지 않습니다. 이 경우, 제 알고리즘에서는 시간복잡도가 $O(2mk-k^2)$ 이 됩니다. 이는 $m$ 과 $k$ 에 대해 단조증가입니다. 그런데 대충 보니 $m$ 은 문제에서 제시한 최댓값정도인 듯하고, $k$ 는 가능한 모든 문자를 사용했으므로 또한 최댓값이 됩니다. 그래서 이것이 가능한 입력 중 최악의 입력케이스였습니다.

$O(n)$ 접근

근데 한참 고민하다 보니까, 그냥 해결책이 떠올랐습니다. dp배열을 저렇게 구상할 게 아니라, 이렇게 하면 어떨까?

dp[i]=i번째 문자열을 끝으로 하는 반복되는 문자가 없는 가장 긴 부분문자열의 시작 위치

그리고 딕셔너리 la를 만들어서, 다음과 같이 정의합니다.

la[x]=현재 위치 이전에 문자 x가 나타난 마지막 위치. x가 한 번도 만약 나타나지 않았으면 0.

이렇게 하면 다음과 같은 알고리즘을 사용할 수 있습니다.

부분문자열의 최대 길이를 maxLength=0이라 두자.
위치 i에서 문자가 x라 하자.
만약 마지막으로 x가 나타난 위치가 dp[i-1]보다 작다면, 이는 dp[i-1]에서 i사이에는 중복된 문자가 하나도 없다는 뜻이다.
- 그러므로 dp[i]=dp[i-1]
만약 마지막으로 x가 나타난 위치(la[x])가 dp[i-1]보다 크다면, 이는 la[x]+1과 i사이에는 중복된 문자가 하나도 없다는 뜻이다.
- 그러므로 dp[i]=la[x]+1
i-dp[i]+1이 maxLength보다 크다면 maxLength=i-dp[i]+1.

사실 이 알고리즘을 다시 한 번 살펴보면 dp배열에서 오직 i-1번째 인덱스에만 접근한다는 것을 알 수 있습니다. 그러므로 dp는 굳이 배열로 구성할 필요 없이 그냥 변수 하나로 둬도 무방합니다.

따라서 다음과 같이 코드를 작성해봤습니다. 아래 코드에서 av가 dp와 같은 의미입니다.

class Solution(object):
    def lengthOfLongestSubstring(self, st):
        l = len(st)
        if l<2:
            return l
        la = {st[0]:0}
        av = 0
        ml = 0
        for i in range(1,l):
            if st[i] in la:
                av = max(av,la[st[i]]+1)
            la[st[i]]=i
            if (i-av)>ml:
                ml = i-av
        return ml+1

코드가 훨씬 짧고 간결해졌습니다.

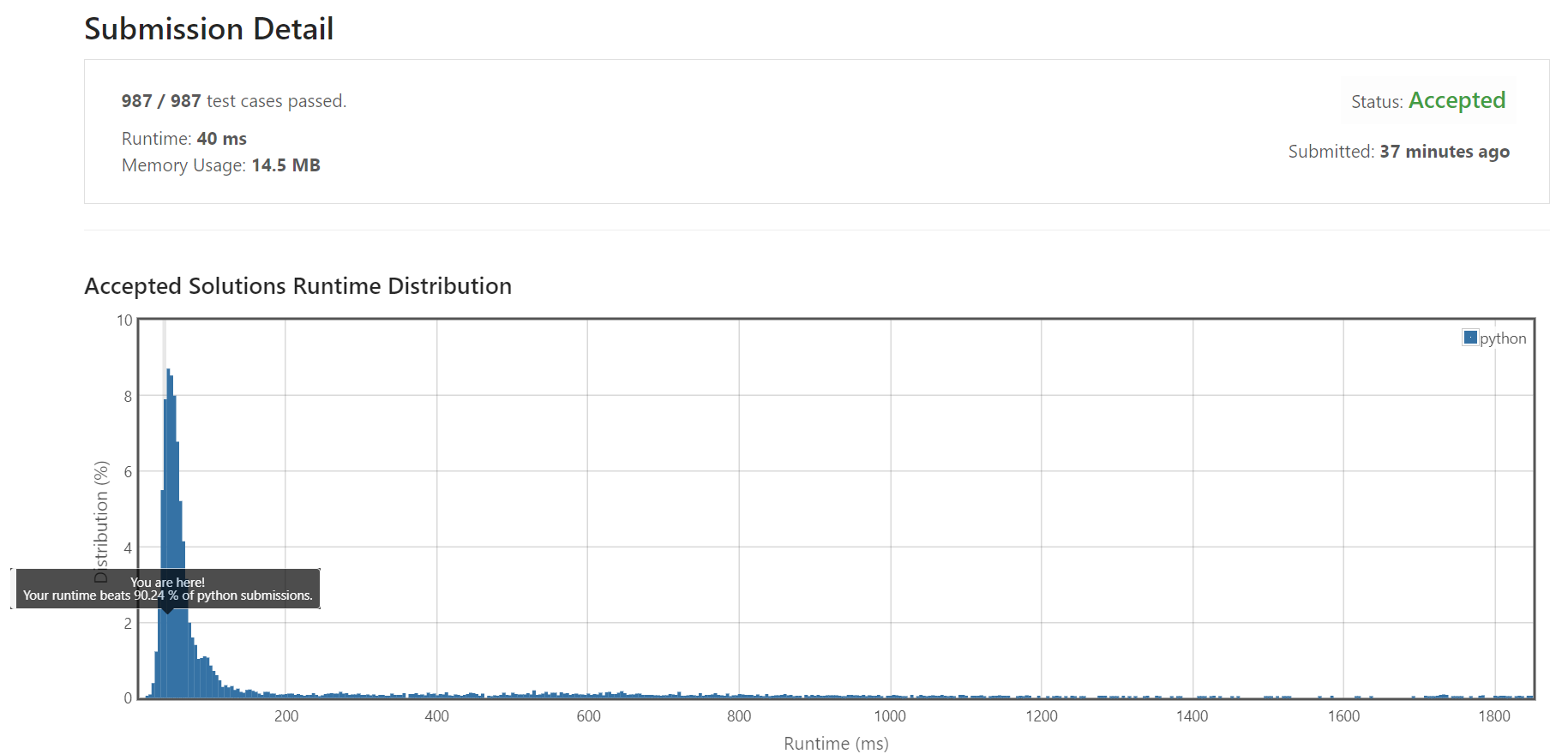
제출 결과, 모든 케이스를 통과했고 상위 10%정도 실행 속도라고 하네요. ㅎㅎ

아래쪽에는 사용한 메모리에서 어느 정도 위치에 있는지를 보여주는데요.

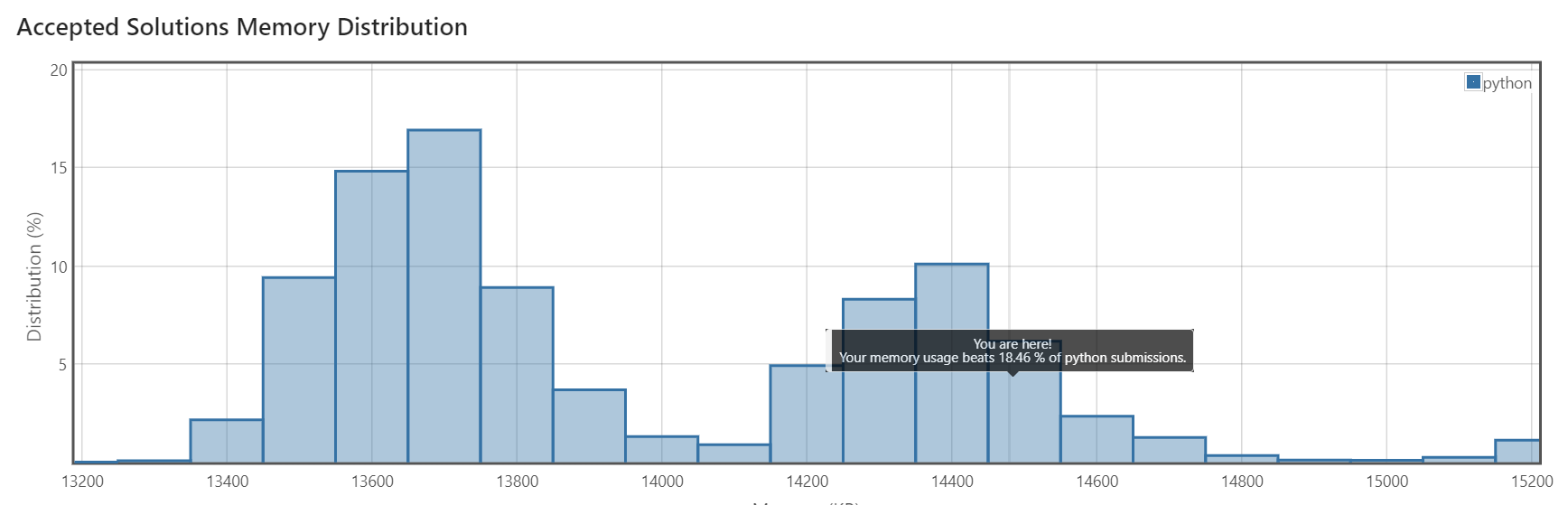
흠... 뭔가 제가 모르는, 메모리를 더 적게 사용하는 방법이 있나 봅니다. 어쨌든 통과했고... 빠르면 된 거 아니겠습니까.ㅎ

메모리도 그래프가 저렇게 생겨서 그렇지, 5%정도밖에 차이가 나지 않습니다. 그런 걸 보니 뭔가 변수 하나 더 쓰고 말고 정도의 차이인가 봅니다.

알고리즘:부분문자열

O(n2)O(n^2)O(n2) 접근

O(n)O(n)O(n) 접근

$O(n^2)$ 접근

$O(n)$ 접근